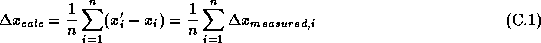
例えば、位置を合わせることを考える。
フレームが2枚の場合はフレームの重なり部分に含まれる星の座標を使って、
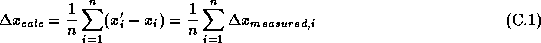
のように一方のフレームに対してもう一方のフレームをずらすべき量が 計算できる。 これは
とした時の残差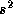
を最小にするための条件である。
このことから、もっと多くのフレームをつなぎ合わせる時には
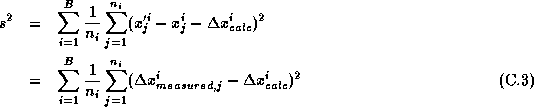
を最小にすれば良いと考えられる。
ただし、フレームの重なり部分の数をB、i番目の重なり部分に含まれる
星の数を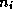
としている。しかし、これは各フレームの重なり部分について別個に
式(1)を適用してずらすべき量を決めるのと同じである。したがって、
次のような問題を生じる。
2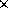
2の4枚のフレームに着目すると
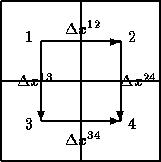
フレーム4のフレーム1に対する相対位置は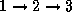
と
たどった時(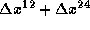
)と
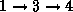と
たどった時(
)では一般に異なる。
これは各重なり部分でずらすべき量が勝手に決められているためである。
このような不都合を生じないためには各重なり部分でのずれが一周した時に
ゼロ(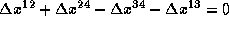
)に
なるようになっていれば良い。
そこですべてのこのような4枚のフレームの組に対して一周した時にずれが
ゼロになるような条件を課しておけばフィールド全体に渡ってあるフレームに対する
別のフレームの相対位置はどのようなパスを通って計算しても同じになる。
この条件は式(3)に次のように別の項を付け加えることで式の形で取り込むことが できる。
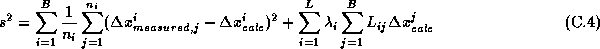
ここでLは4枚のフレームの組(ループ)の数、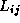
はL行B列の行列で
j番目の重なり部分がi番目のループに含まれているかどうかを示し、
含まれていない時はゼロ、含まれている時は1または-1である(上の例でいえば、
1と2,2と4の重なり部分に対して1とすれば、1と3,3と4の重なり部分に対しては-1と
する)。また、
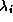はラグランジュの未定係数である。
この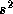
が最小になるように各重なり部分でのずれの量を求めればよい。
この考え方は位置に限らず回転のずれやフラックスに対しても用いることができる。