この作業の目的はモザイクＣＣＤで得られたフレームをつなぎ合わせることですが，その際重要なのは，天体の位置と明るさの誤差を全体に均等にふりわけることです．
また同時に、つなぎ合わせはフィールド全体でconsistentでなければなりません．(あるフレームの別のフレームに対する相対量は一意的でなければならない)．
前者の条件は最小自乗法を用いることで実現します．
後者の条件は2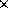
2の隣合う4枚のフレームを順にたどっていった時に各フレーム間の相対量の和がゼロになるような拘束条件を課し，その残差が最小になるようにx,y方向の平行移動量，回転，および明るさの補正量を決めるというラグランジュの未定係数法を用いることで実現します．
具体的に数式で表現すると以下のようになります．
ここで、Bは隣合うフレームが重なった部分の数、Lは2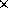
2のフレームの組(ループ)の数、
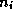はi番目のフレームが重なった部分に含まれる天体の数、
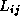はi番目のループにj番目のフレームが重なった部分が寄与しているかどうかの情報を含む行列、
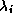はラグランジュの未定係数です．
この残差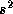
を最小にするように各フレーム間での相対量
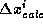を計算
すれば上で述べた条件を満たして各フレームを1枚につなぎ合わせることができます．
またその基となるフレーム間の天体のマッチングは，それぞれのテーブル内の星の位置 からあらゆる3点をとりだし3角形を作り，その辺の長さと2辺のなす角度から，フレーム同士の回転角度を含めた位置関係を決定します． 各モザイクの絵を重ねる範囲と，比べる星の明るさの範囲はパラメータとなっています．